前向传播和反向传播

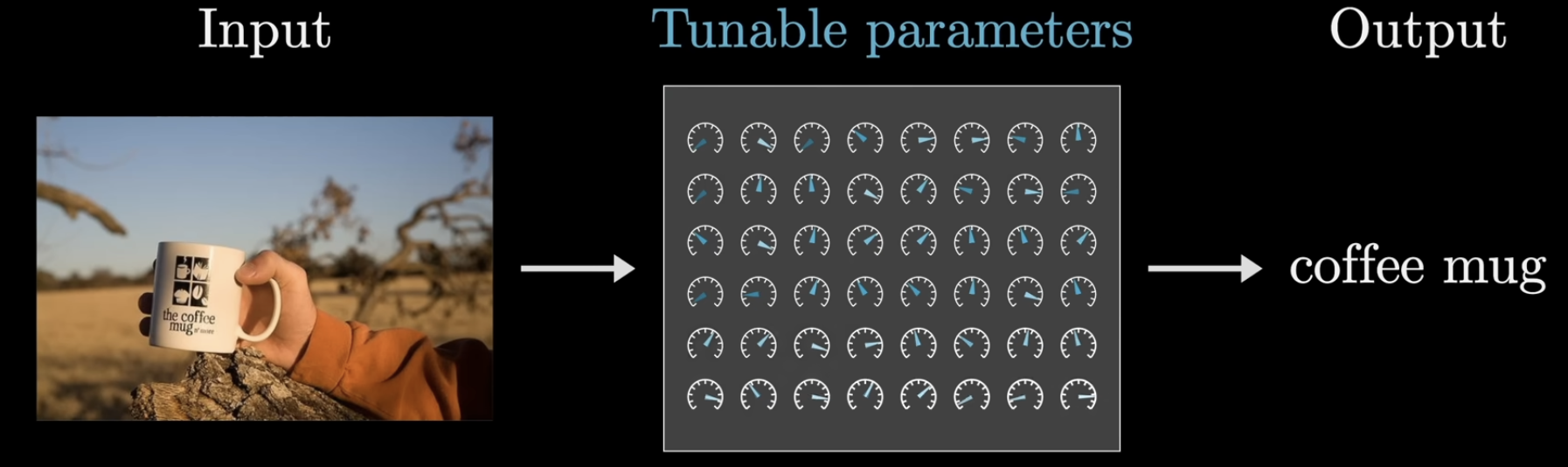
alt text
图片来源

神经网络，是一种模拟人脑神经元网络的计算模型。它由多个神经元组成，每个神经元通过权重和偏移，对输入信号进行处理，最终输出结果。
如上图示，每个神经元就像是一个仪表盘，它通过输入的值，经过处理，最终输出一个值。训练过程，就是在调整这些仪表盘的参数，使得输出尽可能接近目标输出。

前向传播

如前图所示，前向传播的过程就是从输入层到隐藏层再到输出层的过程。

隐藏层

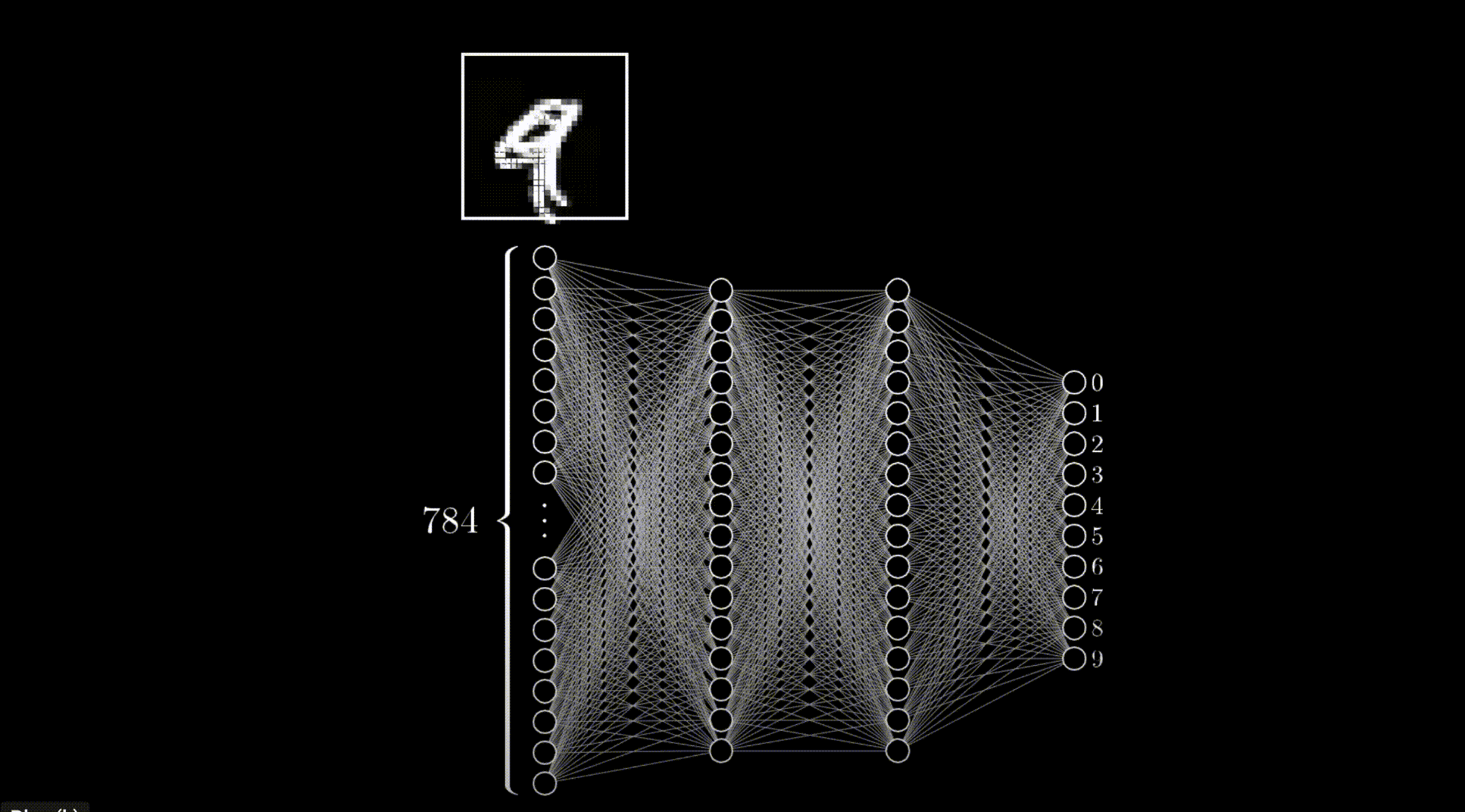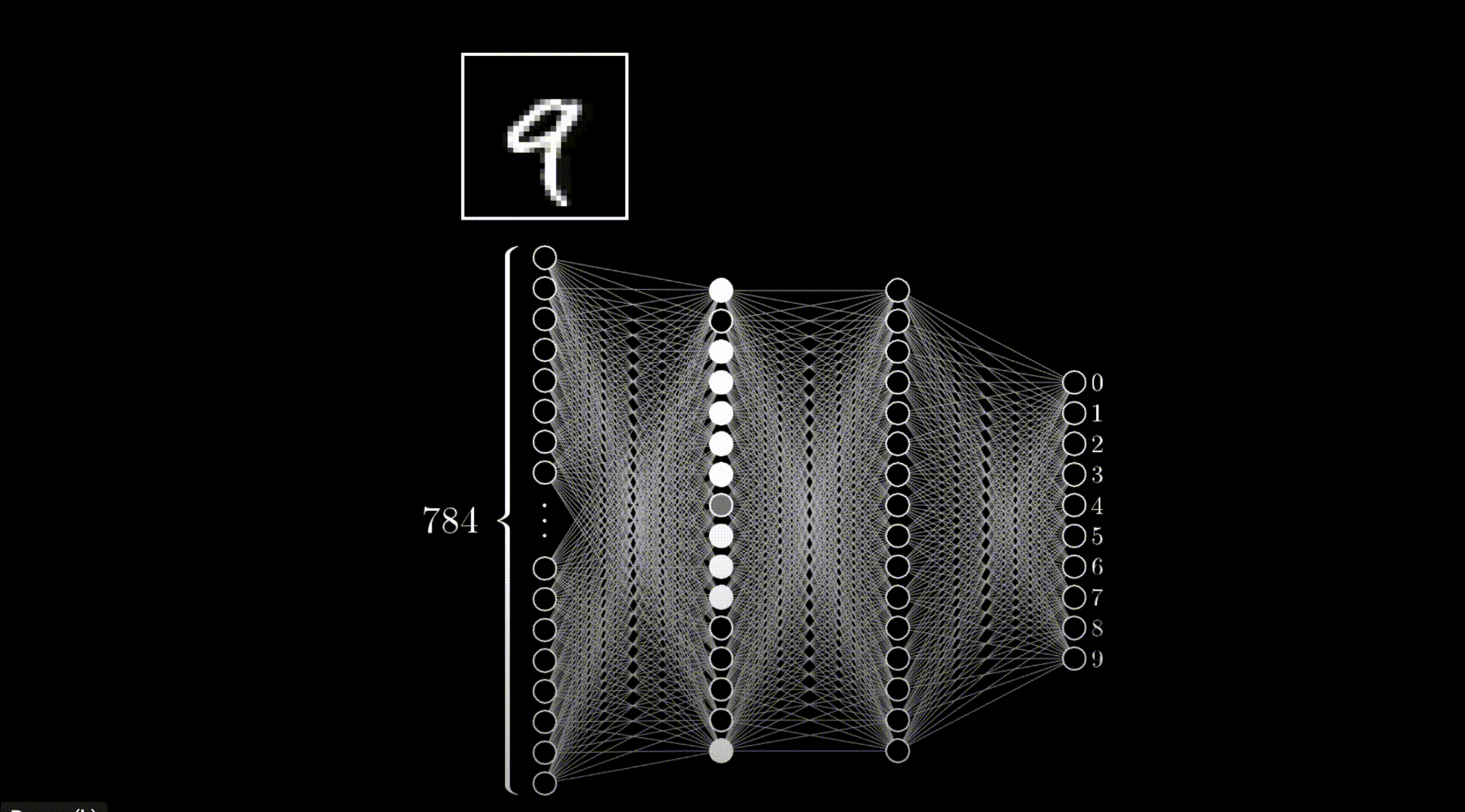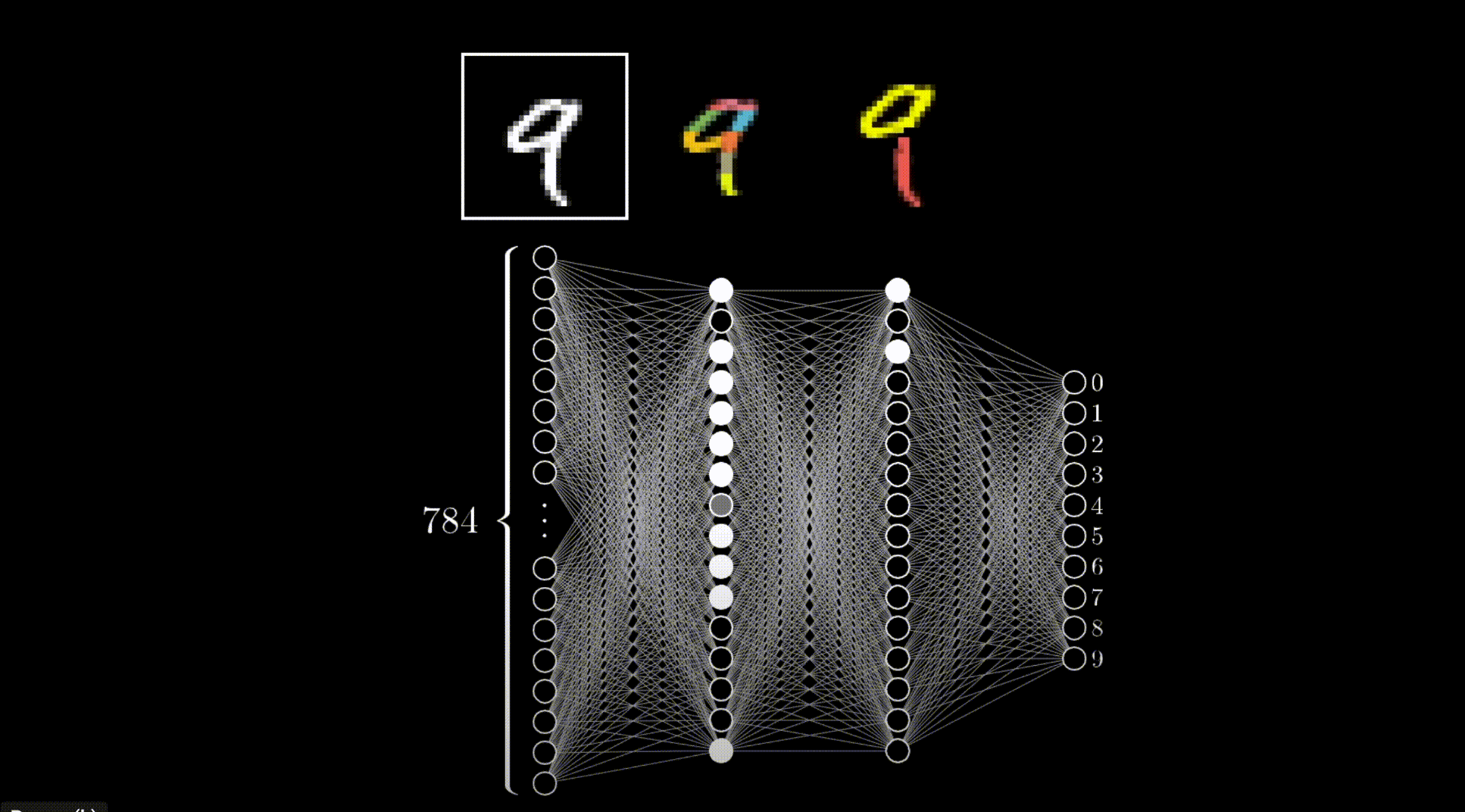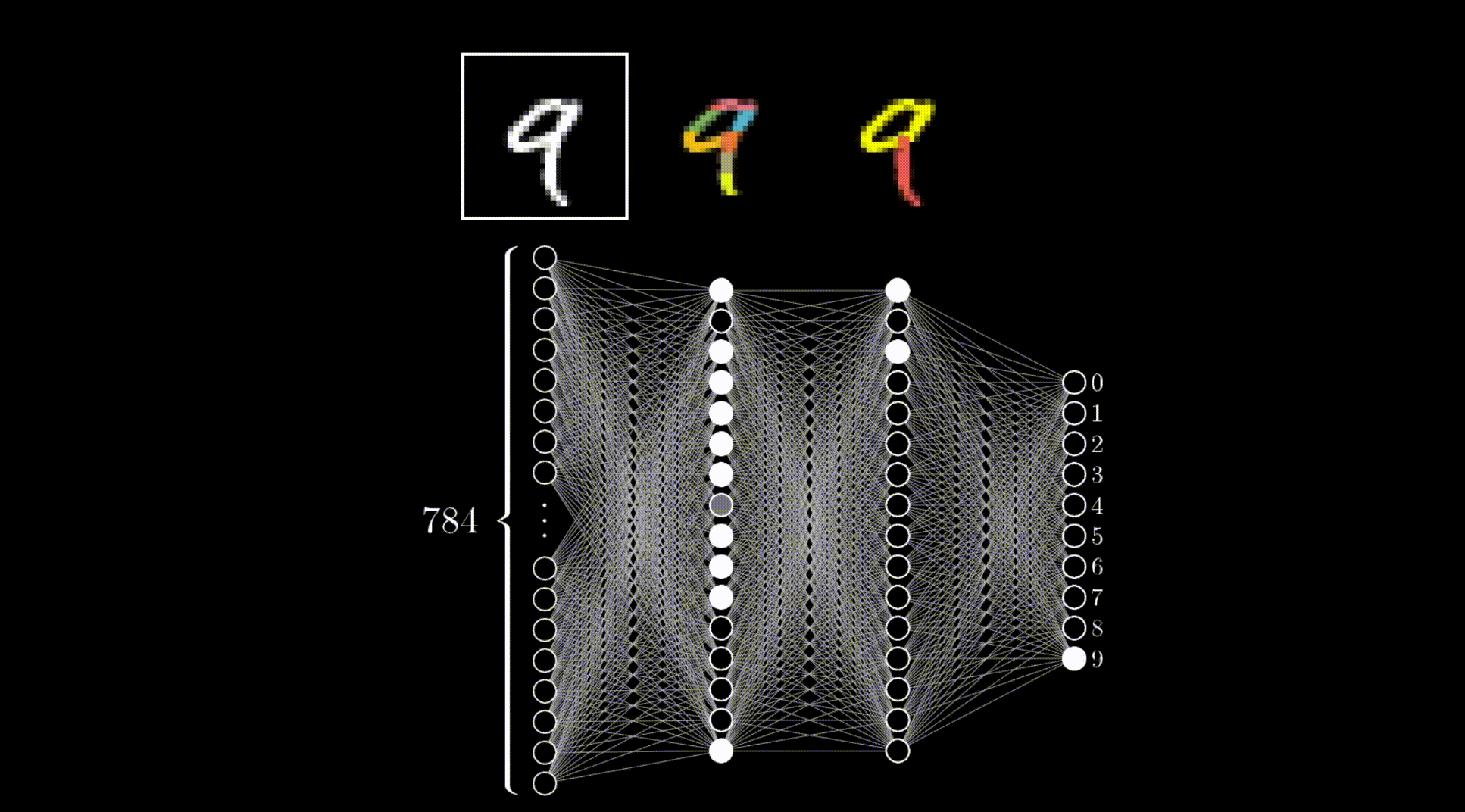
alt text
隐藏层由多层神经元矩阵组成。第一层矩阵中的每个神经元与输入层相连，最后一层矩阵中的每个神经元与输出层相连，中间每层矩阵中的每个神经元都与上一层矩阵中的神经元相连，构成所谓的 全连接。
每个神经元中，我们可以使用一个简单的线性函数来表示神经元的输出，即：y = wx + b。这种函数的好处在于其描述的关系足够简单，计算的效率会很高。但是，它也有明显的缺点，即：无法描述复杂的非线性关系。
这种情况下，这种拟合无论使用多少层神经元，都只不过是单纯的矩阵运算，无法描述复杂的非线性关系，因此，我们需要引入激活函数来描述这种非线性关系。

权重和偏移

y = wx + b 这个公式中，w 是权重，b 是偏移。
权重，说明神经元对输入的敏感程度，权重越大，说明神经元对输入的敏感程度越高。它放大了输入的值。
偏移，反映了神经元的基础激活偏向。偏移越大，更容易激活神经元。
权重和偏移的初始值，通常是随机生成的，因此，我们需要通过训练来调整这些参数，使得神经网络的输出尽可能接近目标输出。显而易见的，权重和偏移越大，y 的值越大。

激活函数

激活函数是一个决策规则，描述了对输入信号做出反应的过程。它决定了神经元的新号是否会下一个神经元传递或者传递多少。
常见的激活函数比如 ReLU、sigmoid（一个更温和的决策者）等。

对于 ReLU 来说，如果输入的值大于 0，则输出输入的值，否则输出 0。
对于 sigmoid 来说，如果输入的值大于 0，则输出 1，否则输出 0。
可以看到，实际上 激活函数引入了非线性关系，使得神经网络可以描述复杂的非线性关系。

反向传播

在前向传播中，输入通过层层神经元矩阵，最终得到输出。但是，这通常会存在很大的误差。我们需要通过反馈调节，调整各个神经元中的参数，以期望误差尽可能小。

反向传播的过程，在层层神经元矩阵中，从输出层开始，逐层向前，计算每个神经元对误差的贡献，并根据贡献调整权重和偏移，以期望误差尽可能小。

这其中，有两个问题需要被解决：

参数该朝哪个方向调整
参数该调整多少

这也就引入了新的概念：损失函数。我们定义一个损失函数，来量化误差，并通过损失函数，我们可以计算出参数的调整方向和调整量。

损失函数

损失函数，描述了输出与目标之间的误差。常见的损失函数比如 均方误差（Mean Squared Error, MSE）、交叉熵（Cross Entropy, CE）等。

MSE

公式如上，我们可以看到，其优势包括：

计算简单，易于理解
曲线光滑，便于求导
凸函数，便于找到最优梯度
对大误差更敏感
它也存在着诸多缺点，比如，对小误差不敏感，对大误差更敏感；假设误差分布呈正态分布等。所以，最终选择哪种损失函数，需要根据实际情况来决定，MSE 通常用于回归问题（拟合输入特征和连续输出之间的映射关系）。

我们可以看到，实际上，输出和目标值之间直接的误差只发生在最后一层，也就是输出层。输出层的误差会通过反向链式法则，逐层向上影响。造成最终误差的结果，是所有层误差的累加。

最后一层的 MSE 公式如下：

x 是输入，w 是权重，b 是偏移。我们要调整的是 w 和 b。这里，w 和 b 的调整方向，是使得 y 尽可能接近 target。所以，w 和 b 才是这里的变量。最终，这个最小误差问题，就转换成了求解这个公式中，能够让 MSE 最小的 w 和 b。这两个变量是通过梯度下降法来求解的。

梯度及参数更新

梯度是个向量，方向指向函数值增加最快的方向，大小表示函数变化的速率。对于上述的 MSE 公式，我们可以求出其梯度，即：

在隐藏层中，误差无法直接传播，因此，我们需要通过链式法则，将误差传递到隐藏层。最终的误差，隐藏层也负有责任。
同样，我们假设激活函数是线性的，来考虑误差是如何在隐藏层中传递。

示例

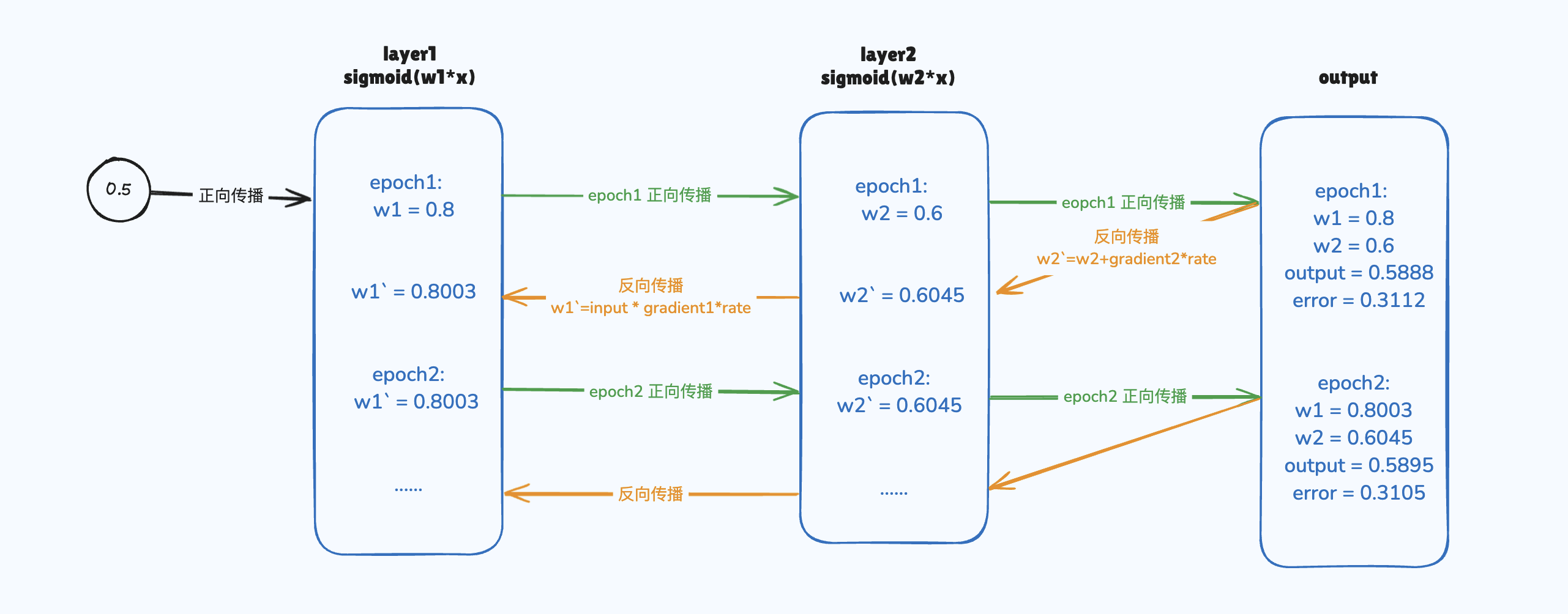
train-process

import numpy as np

def sigmoid(x):
    # sigmoid激活函数
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    # sigmoid函数的导数
    return x * (1 - x)

# 初始化参数
input_value = 0.5  # 输入值
weight1 = 0.8  # 第一层权重
weight2 = 0.6  # 第二层权重
target = 0.9  # 目标输出值
learning_rate = 0.1  # 学习率

print("训练开始！")
print(f"初始输入: {input_value}")
print(f"目标输出: {target}")
print("--------------------")

# 进行3轮训练
for i in range(1000):
    # 前向传播
    layer1 = sigmoid(input_value * weight1)  # 隐藏层输出
    output = sigmoid(layer1 * weight2)  # 最终输出
    error = target - output  # 计算误差

    gradient_output = layer1 * error * sigmoid_derivative(output)
    error_at_hidden = gradient_output * weight2
    gradient_hidden = input_value * error_at_hidden * sigmoid_derivative(layer1)

    # 更新权重
    weight2 = weight2 + gradient_output * learning_rate
    weight1 = weight1 + gradient_hidden * learning_rate

    print(f"第{i + 1}轮训练:")
    print(f"预测输出: {output:.4f}")
    print(f"当前误差: {error:.4f}")
    print(f"weight1更新为: {weight1:.4f}")
    print(f"weight2更新为: {weight2:.4f}")
    print("--------------------")

风雪围城