
回顾一下,在 上一篇文章中,我们提到了在反向传播过程中的梯度计算。
梯度,是损失函数(成本函数)对参数的偏导数组成的向量。它的方向是损失函数上升最快的方向,它的值是损失函数上升最快的速率。
如上图示,是一张3D的损失函数图,其中,x轴和y轴分别是参数 w 和 b,z轴是损失函数的值。我们最终的目标是希望损失函数最小,即找到最优的参数 w 和 b。
这就像是一个下山的过程,我们需要找到那个下山最快的方向,但是,山路是曲折的,我们需要不断的调整方向,逐步跨步(按照一个学习率)。跨步太大,可能会错过最优解,跨步太小,可能会收敛太慢。
当然,实际过程要复杂的多,在神经网络中往往会存在很多的隐藏层,而每一层都需要计算梯度,而每一层的梯度计算都需要依赖于前一层的输出以及对后一层结果产生的影响。影响可能会被放大,也可能会被缩小,这就是梯度消失和梯度爆炸的本质原因。
为什么需要这么多的隐藏层
对于单层神经网络,就像是要求一个人一眼就认出一张图片中的猫,这显然是困难的,实际上,我们是通过各种特征进行的识别。比如,猫的耳朵、眼睛、鼻子等。同理,对于神经网络而言,也需要通过多层神经网络,来提取出更多的特征,从而更好的完成识别,这是应该是一个渐进的过程。
我们可以想象,第一层的神经网络主要用于感知。识别出图片的颜色、轮廓等基本纹理和边缘。
第二层的神经网络主要用于组合,将第一层识别出的特征进行组合,形成更复杂的特征。比如,识别耳朵、眼睛、鼻子等。
在更深层次的抽象中,往往会基于已有特征抽象出更高级的特征。比如,一对耳朵、毛茸茸的脸等。
最终,神经网络会综合所有特征,做出决策。
这种多层网络具有巨大的优势:
- 特征分层学习。每一层都在学习、提取更高级、更抽象的特征,从简单到复杂,逐步构建。
- 非线性表达能力。通过多层的堆叠,可以构建出非线性的表达能力,从而更好的拟合复杂的物理世界。
- 鲁棒性(抗干扰能力、稳健性)。多层网络能够学习到更稳健的特征表达,对输入的细微变化更加不敏感。比如,如果只是光线稍微暗一点,神经网络也能够识别出这是猫。
- 泛化能力。深层网络能够学习到更本质的特征,而不是简单记住训练数据的表面特征。比如,如果只是训练了白色的猫,如果出现了黑色的猫,神经网络也能够识别出这是猫。
那是不是层数越多越好呢?层数越多:
- 计算量越大,计算速度越慢。
- 参数越多,越容易过拟合。
- 越容易出现梯度消失和梯度爆炸。
过拟合
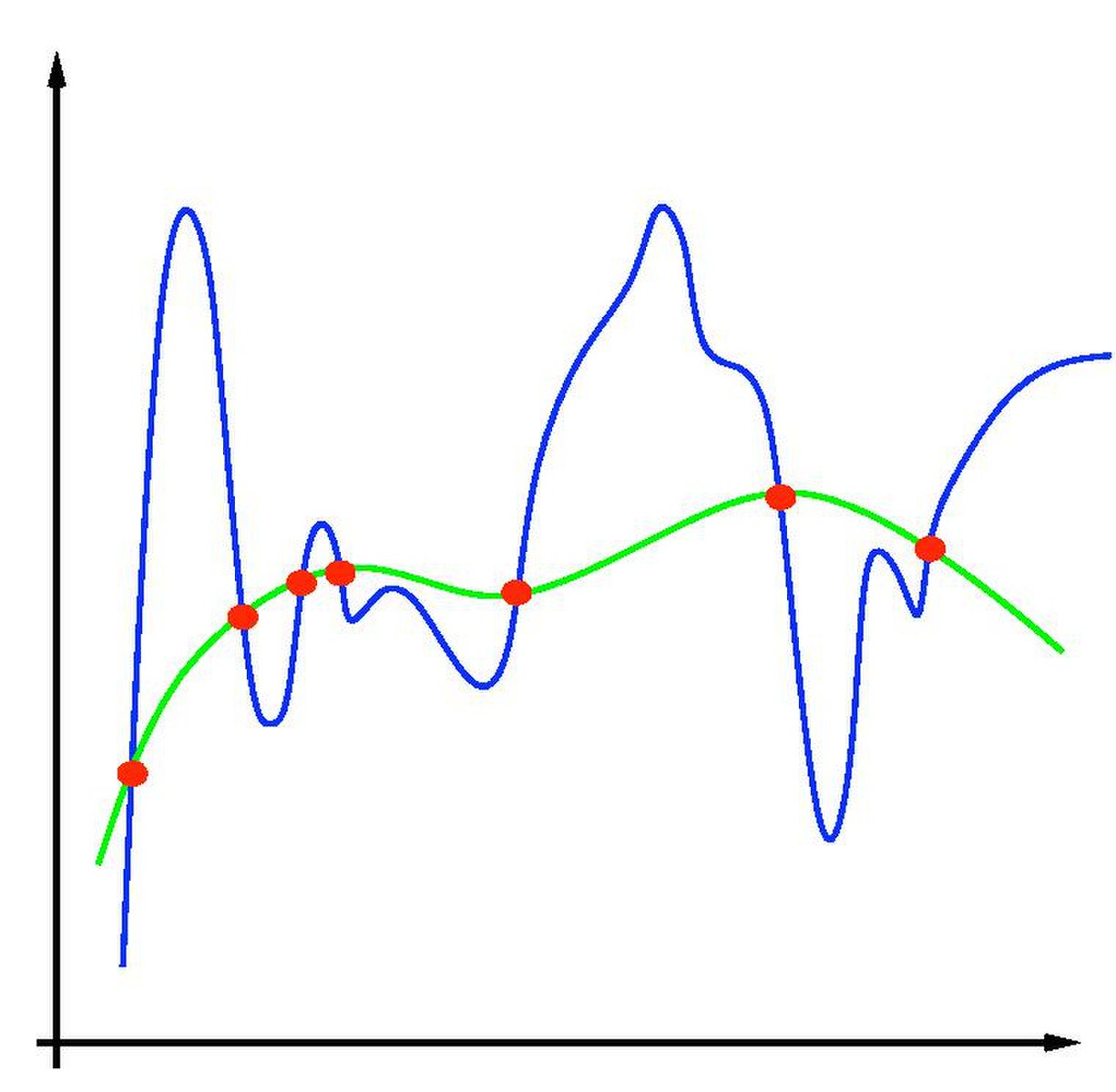
过拟合,是指模型在训练数据上表现得很好,但在未见过的数据上表现不佳的现象。如上图所示,有多种函数可以拟合样本空间的情况,函数可以很复杂,但可能不够平滑,如上图蓝色线表示;函数也可能会比较简单,足够平滑,如上图绿色线表示。波动太大,往往意味着噪声太多,不够泛化,一个入参变大后,输出结果可能会有很大的变化,不够稳定。
这种现象往往是因为模型过于复杂,或者样本数量不够,或训练时长太长,导致模型过度地”记住”了训练数据的细节,以至于学习到了训练数据中的噪声,而不仅仅是数据中的规律,失去了泛化能力。
为了避免过拟合,可以采取以下措施:
- 减少模型复杂度。减少层数或每层的神经元数量(参数)。
- 增加样本数量。如果样本数量不够,可以考虑做数据增强。对于图像识别,可以考虑旋转、缩放、裁剪、翻转、颜色变换等,创造新的样本。
- 增加
正则化项。修改损失函数,给模型增加一些约束或惩罚,从而避免模型过于复杂。 - 早停(Early Stopping)。发现验证集上损失不再下降,尽早停止训练。
正则化的本质,是通过在损失函数中增加一个正则化项(惩罚项),来告诉模型:不要过分追求在训练数据上的完美表现,要保持简单和*泛化能力*,即,给模型增加规范,让模型遵循法则。需要注意的是,这里的正则,并不是指正则表达式,而是指正则化。L_total = L_original + λR(w)
其中,L_total 是新的损失函数,L_original 是原始损失函数,R(w) 是正则化项,λ 是正则化强度。
L1 正则化
R(w) = ||w||₁ = ∑|wᵢ|
这里使用参数的绝对值之和作为惩罚项。
L1 正则化,是指在损失函数中增加一个 L1 范数,即参数的绝对值之和。
- 会将不重要的特征权重直接压缩为 0
- 随着正则化强度增加,模型会倾向于将更多的权重压缩为 0
- 保留的特征往往是重要的特征
L2 正则化
R(w) = ||w||₂² = ∑wᵢ²
这里使用参数的平方和作为惩罚项。
L2 正则化,是指在损失函数中增加一个 L2 范数,即参数的平方和。
- 所有特征权重都会变小,但不会为 0
- 随着正则化强度增加,模型会倾向于将更多的权重接近为 0
- 保留了所有特征,但降低了特征权重
参考链接
梯度下降
“L1和L2正则化”直观理解(之一),从拉格朗日乘数法角度进行理解
什么是 L1 L2 正规化 正则化 Regularization (深度学习 deep learning)
如何解决过拟合问题?L1、L2正则化及Dropout正则化讲解