
词语的位置决定其语义功能,这是 seq2seq 模型必须解决的核心问题。比如,I saw a saw,两个 saw 在不同位置含义完全不同。
Transformer 模型并行处理所有输入词汇,失去了序列的内在顺序。位置编码通过将位置信息注入输入表示来解决这一问题。理想的位置编码应具备两个数学特性:位置的唯一性(不同位置有不同编码)和相对位置的可学习性(位置间的关系可被模型捕捉)。
位置编码的实现
在 Transformer 模型中,位置编码是通过三角函数实现的。编码公式如下:
其中,$pos$ 表示词汇在句子中的位置,$dmodel$ 表示词汇的维度数量,$i$ 表示维度索引(从 0 开始)。指数缩放因子为 $\frac{1}{10000^{2i/dmodel}}$,对三角函数的频率进行控制。
我们以 “cat is sleeping on the mat” 为例,来理解位置编码的实现。
假设,每个词使用一个维度为 5 的向量表表示,那么,这句话的向量表示如下所示: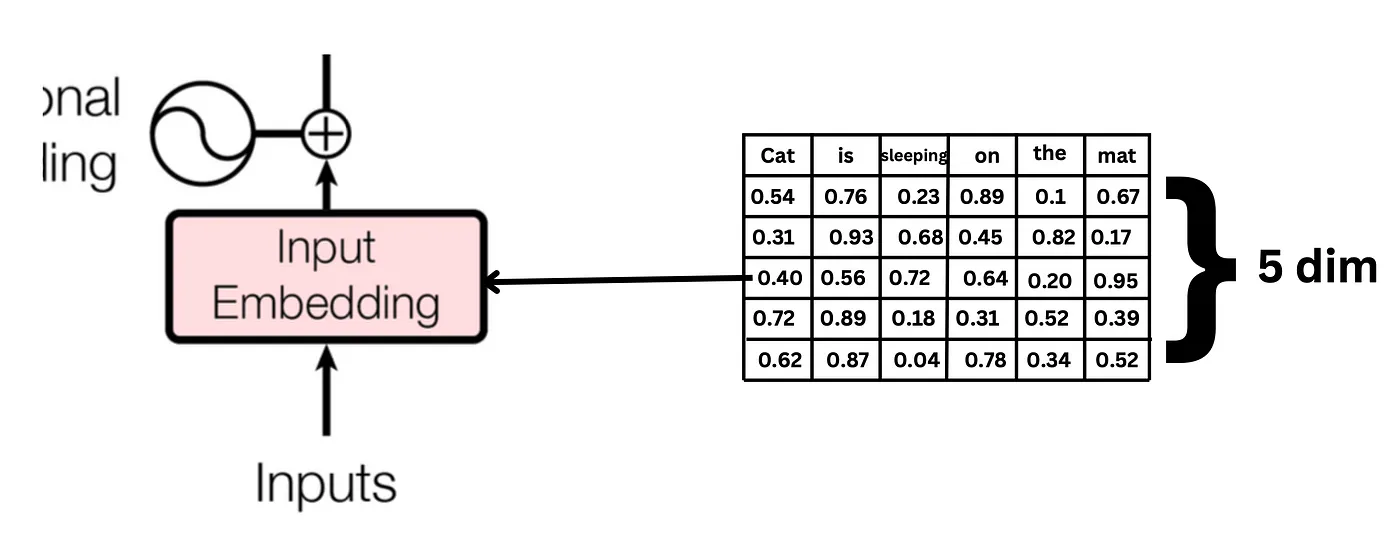
结合位置编码公式,”cat” 的位置编码计算过程如下: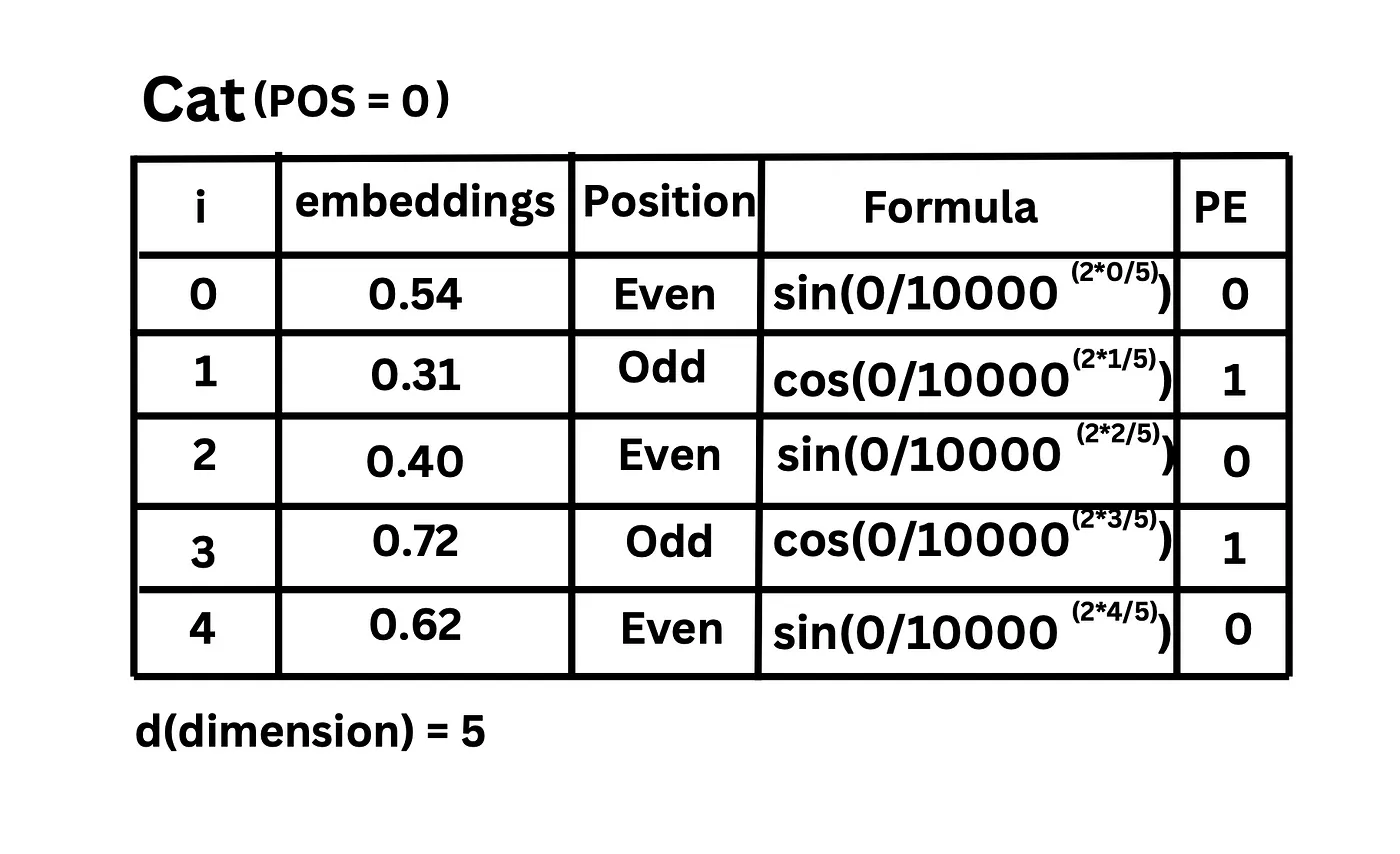
句子中每个词的位置编码如下: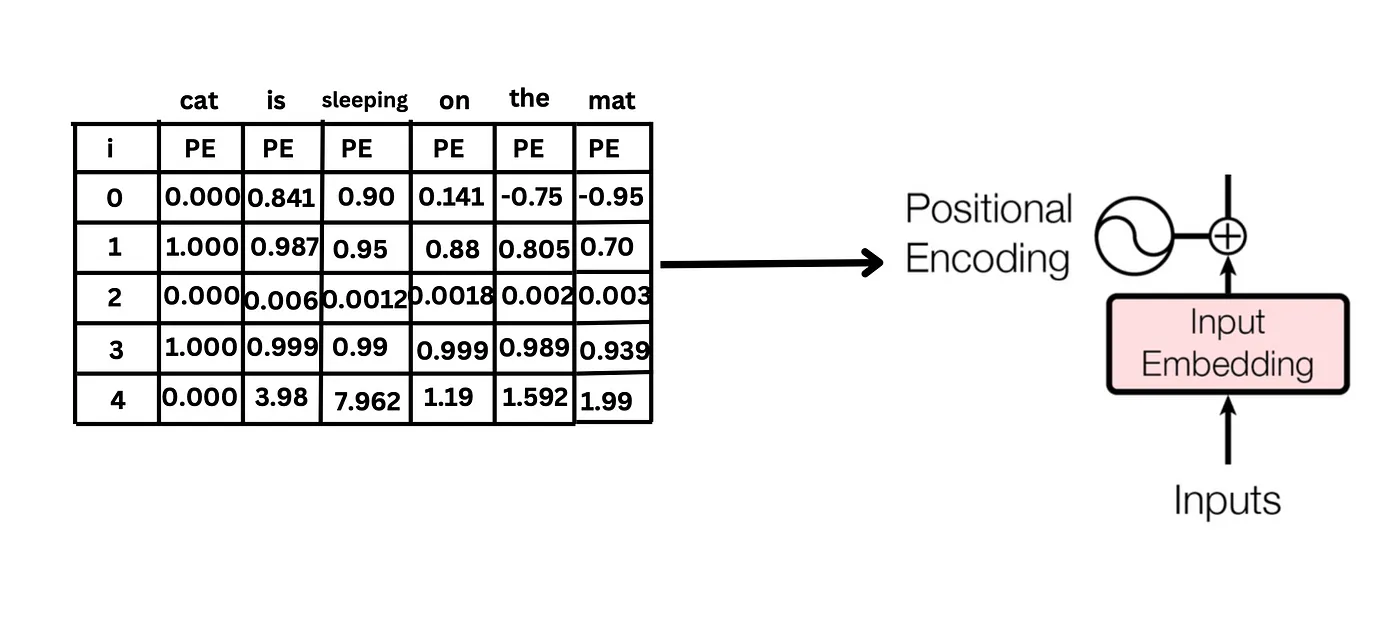
最终,位置编码和 word embedding 相加,得到最终实际的输入向量: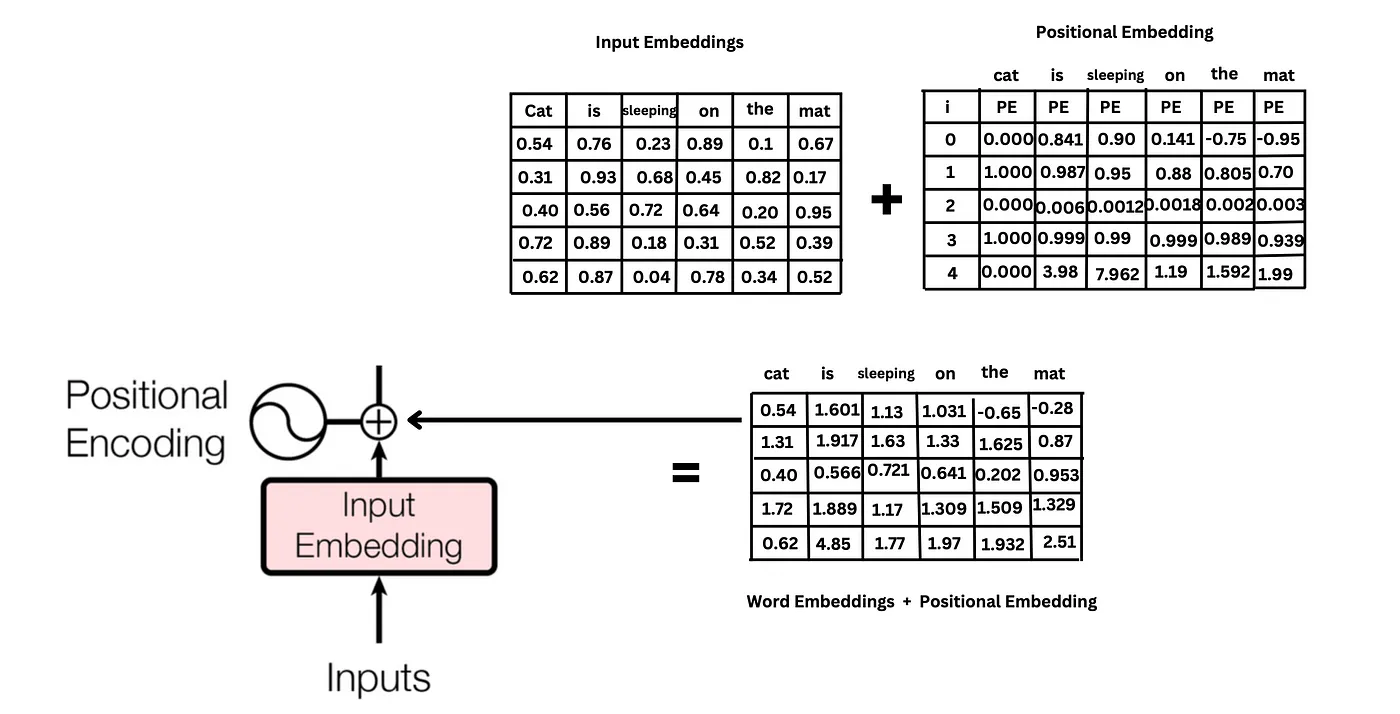
这时,每个词的输入向量,既包含了词义信息,也包含了词在句子中的位置信息。
位置编码背后的机制
为什么要使用 sin 和 cos 函数?
1. 相对位置的线性表达
根据三角恒等式,存在:
在编码计算过程中,同一维度索引下的不同位置向量分量的所对应的函数的频率 $w$,即 $\frac{1}{10000^{2i/dmodel}}$ 是相同的。
因此,通过下述公式,
可以得到

这表明位置 $pos+k$ 的编码可以通过位置 $pos$ 的编码进行线性变换得到,变换矩阵只依赖于 $k$。这种变换是有方向性的,从而能够确定词语的前后顺序关系。
这使得模型可以学习到相对位置关系。相对位置关系,是位置编码的核心。词语的相对位置,决定了句子的语义。
2. 每个词汇位置的唯一性

3. 平滑的距离度量
三角函数编码创建了一个平滑的位置表示。相邻位置的编码非常相似,而相隔较远的词汇的编码差异较大。这也符合自然语言中语义关系的特性。
4. 无限长度的外推能力
如题图所示,三角函数编码具有无限长度的外推能力。这意味着,当需要处理更长的句子时,位置编码仍然能够保持良好的性能。
缩放因子的作用
缩放因子可以控制三角函数的频率。
在位置编码公式中:
$$PE_{(pos,2i)} = \sin(pos \cdot \frac{1}{10000^{2i/dmodel}})$$
$$PE_{(pos,2i+1)} = \cos(pos \cdot \frac{1}{10000^{2i/dmodel}})$$
这里的 $\frac{1}{10000^{2i/dmodel}}$ 就是角频率 $\omega$,它决定了正弦/余弦函数完成一个周期所需的位置变化量。
可以看到,这个缩放因子随着维度索引 $i$ 的增加而指数级减小:
当 $i=0$ 时,频率为 $\frac{1}{10000^{0}} = 1$
当 $i=dmodel/2-1$ (最大维度索引) 时,频率接近 $\frac{1}{10000}$
这种指数级的变化创建了一个频率梯度,使得不同维度能够捕捉不同尺度的位置关系:
- 低维度(小的 $i$ 值):高频,捕捉局部、短距离的位置关系
- 高维度(大的 $i$ 值):低频,捕捉全局、长距离的位置关系
当然,虽然频率提供了表达不同尺度位置关系的能力,但最终这些信息的有效利用,确是需要依赖模型参数矩阵来调节和学习。