
计算机世界需要用数学语言来描述和拟合现实世界的规律。某种程度上,这些规律本身就像是一个待我们去发现的复杂函数。
如下图示,我们可以将 Transformer 看做是一个函数黑盒,它实现了”下一个词”的预测,就像是学会了人类的表达。
在 Transformer 内部,前馈神经网络是 Transformer 的重要组成部分。它也是一种强大的函数拟合工具。
通过构建非线性网络结构,它能够逼近现实世界中的复杂规律。
它就像是一个特征加工车间,通过两道工序处理信息:
- “特征展开”,为了便于”观察”,将输入信息投射到一个更大的空间,并通过ReLU激活函数突出重要特征,就像在显微镜下观察时调整焦距,让细节更加清晰;
- “特征提炼”,将重要信息提取出来,形成最终的特征表示。这种设计让FFN能够学习到更丰富的特征转换关系。
“提炼”出来的特征,使得模型能够精准地理解输入信息,并应用于”下一个词”的预测。
前馈神经网络的数学表达
以Transformer中的FFN为例,它可以表示为:
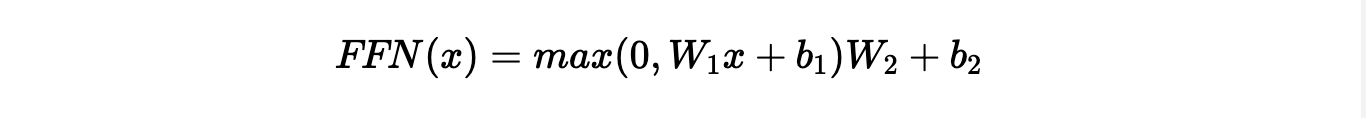
其中:
- x 是输入向量
- W1 是第一个线性变换的权重矩阵,将特征映射到高维空间
- b1 是第一个变换的偏置向量
- max(0, ·) 是ReLU激活函数,保留正值,将负值置零
- W2 是第二个线性变换的权重矩阵,将特征映射回原始维度
- b2 是第二个变换的偏置向量
从这个公式的结构可以清晰地识别出FFN的两个关键阶段:
扩展阶段:xW1 + b1
- 这一步中,W1 通常是一个形状为 [dmodel, dff] 的矩阵,其中 dff 远大于 dmodel
- 例如,在原始Transformer中,dmodel = 512,而 dff = 2048,是模型维度的4倍
- 这种设计使得特征能够投射到更高维的空间,便于捕捉更复杂的特征关系
压缩阶段:(…)W2 + b2
- 在ReLU激活函数处理后,W2 的形状为 [dff, dmodel],将特征空间压缩回原始维度
- 这种压缩不是简单的降维,而是一种信息提炼,保留经过非线性变换后最有价值的信息
- 可以理解为模型在”决定”哪些高维特征是解决当前任务最重要的
这种”扩展-压缩”的设计遵循了表征空间转换的原理:在更高维的空间中,原本难以区分的特征可能变得更容易分离,从而使模型能够学习到更复杂的模式。
从数学角度看,表征空间转换的核心操作之一是矩阵乘法,而矩阵乘法本质上就是对象在空间中的运动,将一个点投射到其他维度上。投射到高维时,为特征分离提供了可能,就像将纠缠在一起的线团展开到更大的空间中,使原本重叠的线条能够分开排列,从而更容易识别每条线的走向和特点(流形假设告诉我们,真实世界的高维数据往往分布在低维流形上,而合适的空间转换可以揭示这种结构);投射到低维时,是将这些特征进一步压缩和提取出来。
一个实际的矩阵计算是: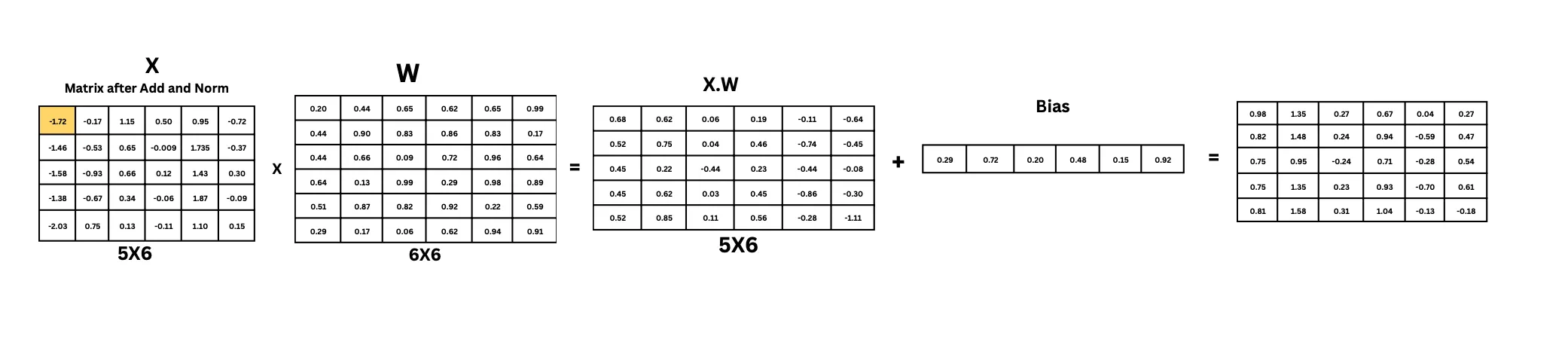
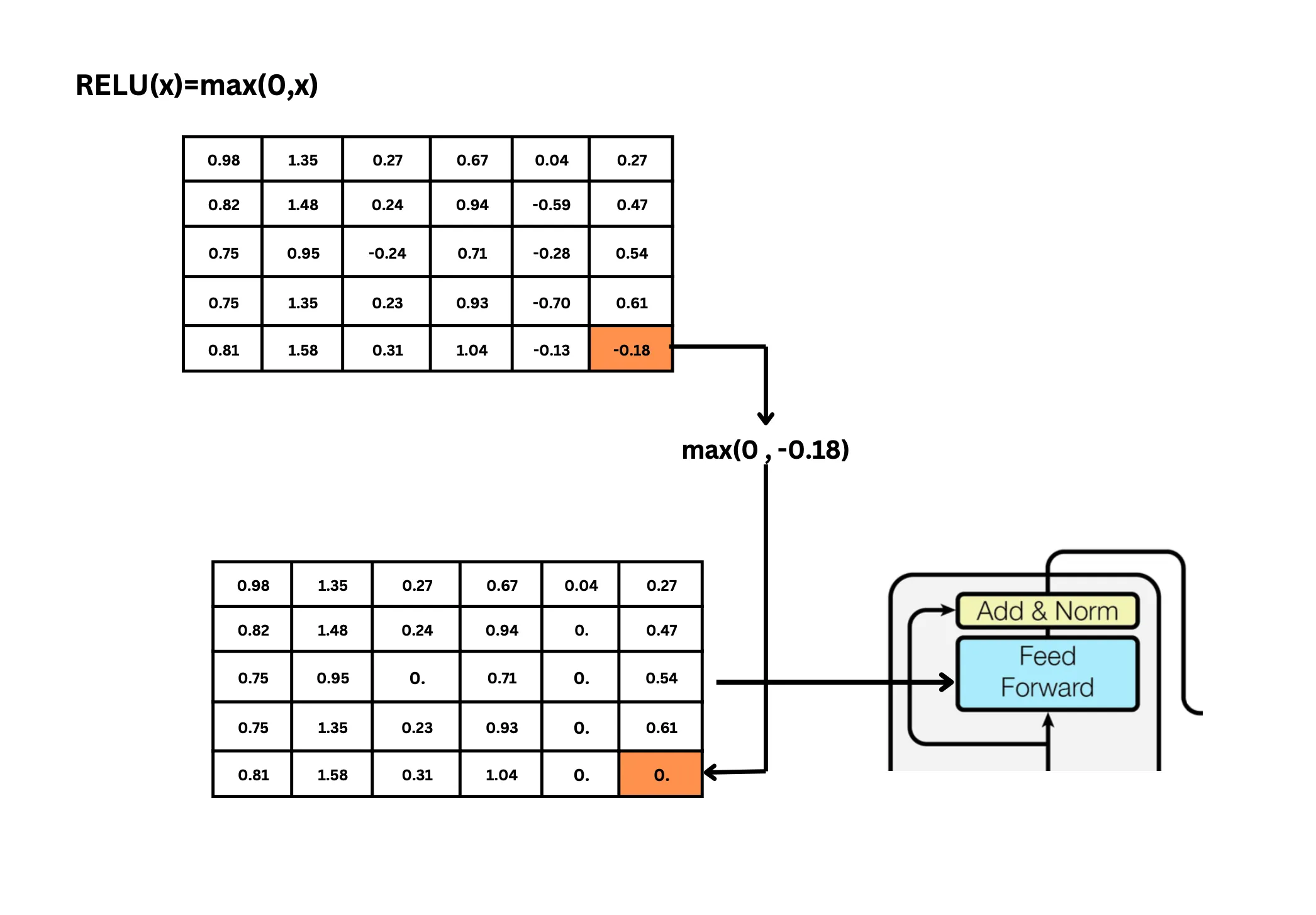
在实际应用中,会使用多个前馈神经网络堆叠,多尺度的进行特征提取。
参考链接
Understanding Transformer Architecture Using Simple Math
ResNet 残差神经网络
为什么transformer的FFN需要先升维再降维?
理解矩阵(二)